Understanding phase lag is important when scanning at high speeds with piezo flexure stages. This article describes the phase relationship between the command signal and the stage response. The response is monitored using the internal (in this case capacitive) sensor. The bandwidth of a system is the key element to phase lag. Using control parameters one can easily obtain a bandwidth of approximately 1/3 the loaded resonance of the system. In general the bandwidth of a system depends on resonance frequency of the stage, the load mass, mounting configuration, as well as a variety of external factors. The system in the following example is purposefully tuned to have a bandwidth of 100Hz for demonstration purposes.
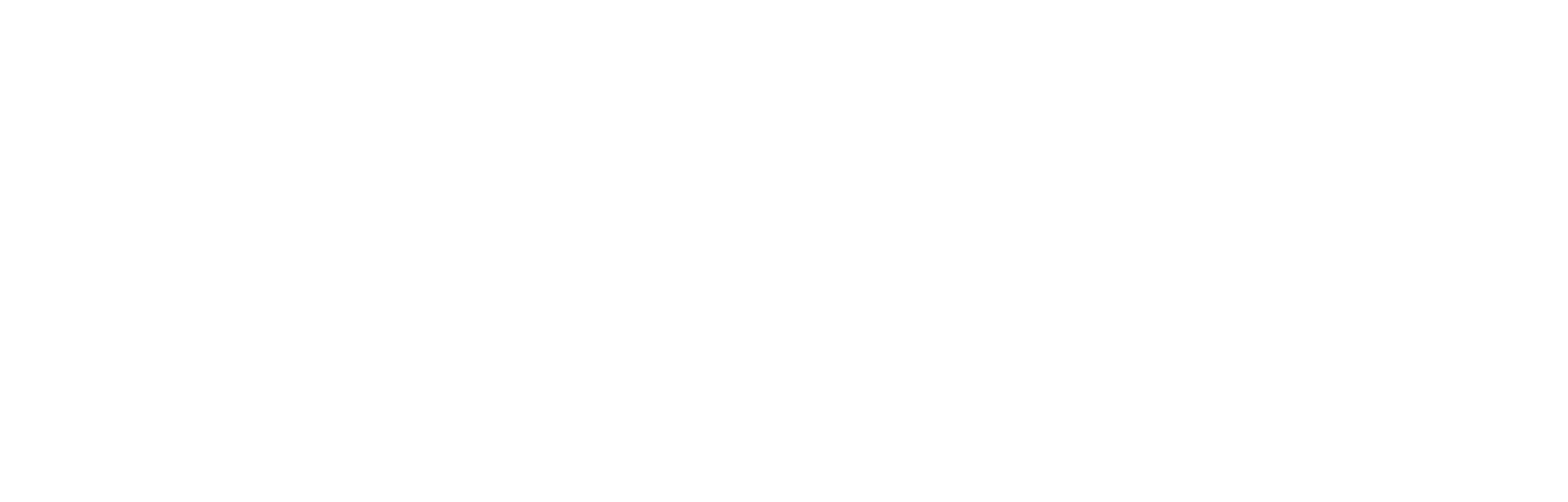
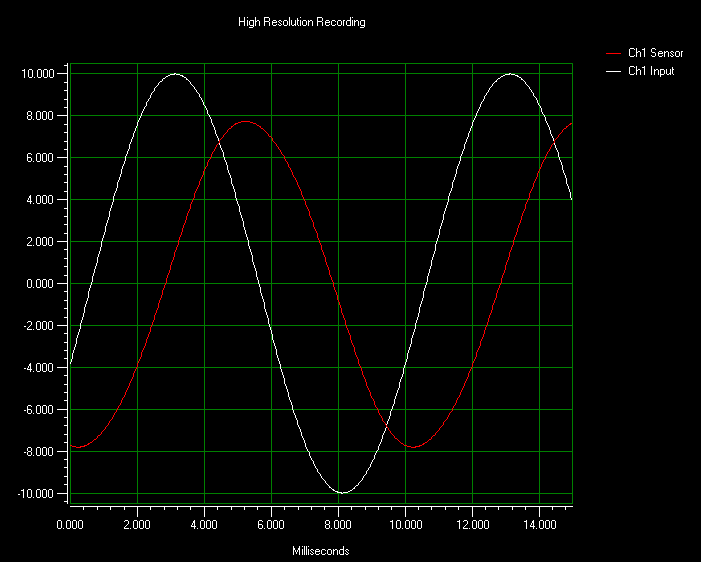
The phase difference is typically measured as the difference between the positive zero crossings, however any two analogous points on the waveform can be used. This is usually expressed in degrees (the difference in zero crossings divided by the total period of the wave multiplied by 360 degrees). The images below illustrate the input (commanded position) and output (sensor reading) pairs for four different scanning frequencies. The data was taken with the nPControl software included with the LC.400 series controllers. Please note that no additional control features were used during this testing, and that tracking error can be reduced further with additional controller features. The results are also listed in the table following the images.
Measuring Phase Lag with nPControl Software
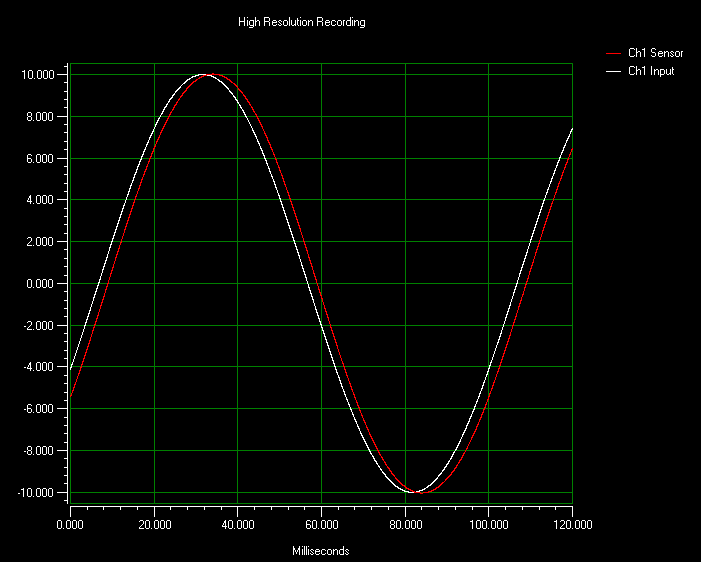
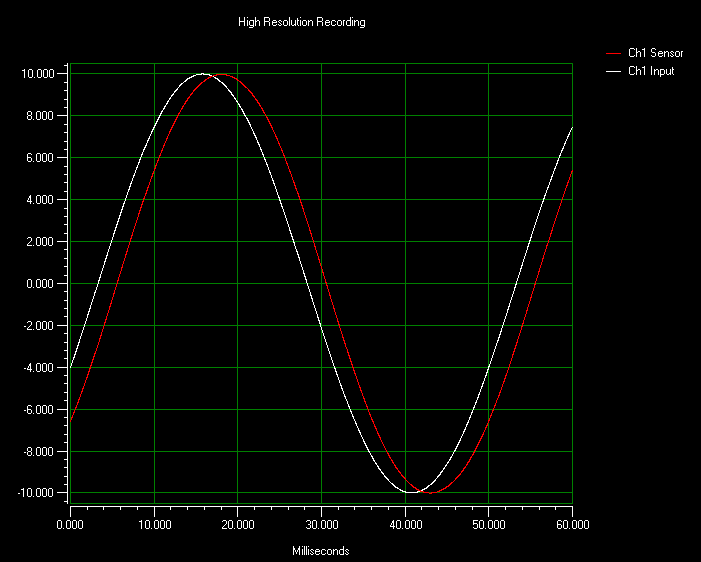
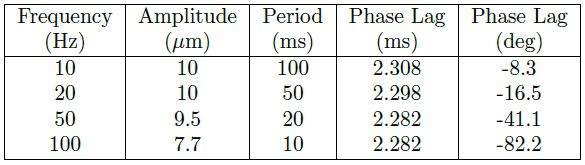
The following chart lists the results obtained from analyzing the four different scanning configurations. Phase lag results at different frequencies can be seen here. Please also note that as the driving frequency increases, the phase lag (in time) stays mostly the same as a consequence of the control-loop tuning, but the lag takes up more and more of the input period.
Relevant Measurements of the Output Sine Wave
Measuring Phase Lag with a Bode Plot
Another way to measure the phase is to use the results of the Fourier Transform (FFT) of a system’s step response. A closed-loop step is measured and the FFT is calculated by the nPoint software. This stage is tuned with approximately a 100Hz bandwidth. The following figures show the magnitude and phase plots of the system.
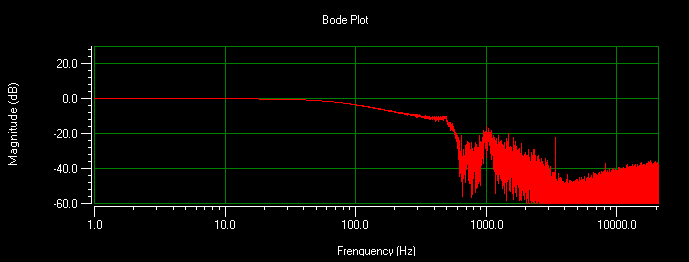
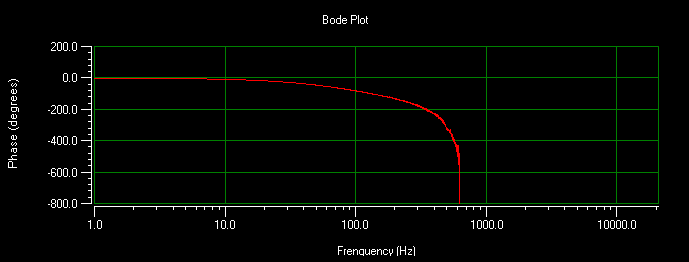
The following plots show the step response of a 100Hz bandwidth system. Magnitude and phase can be seen with these plots. The numbers correspond to what was seen in the actual waveform.
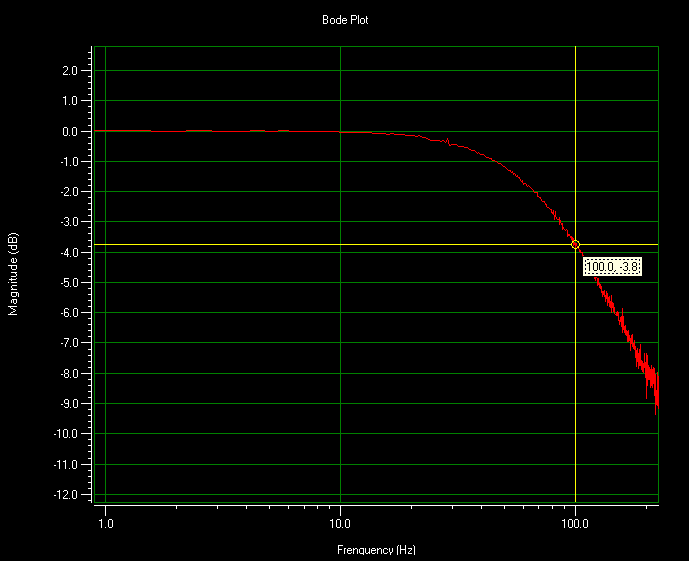
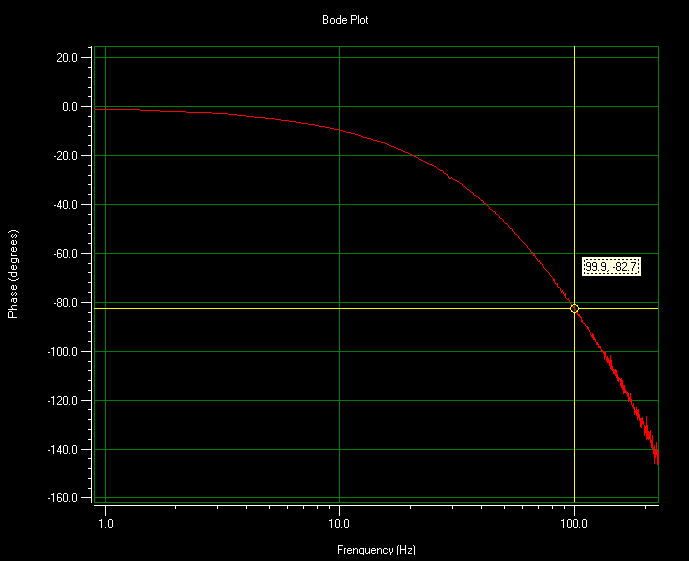
Phase delay can be estimated based on the bandwidth of the nanopositioning system. Although there are control features that can improve this response, it is important to understand how this affects scanning. Many applications that require high-speed scanning use the sensor output to correlate data acquisition with actual position. In this event scanning at higher speeds can occur without the phase lag affecting the results. The nPControl software can give the user an understanding of the phase lag present in a given system so that they can make the necessary adjustments for their application.